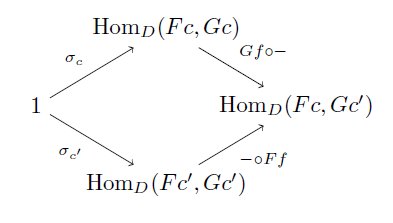V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
C, Dを圏として、関手 T: C^op×C→D を考えます(先に言ってしまうと、TとしてHom(-, -)みたいなものを取ることを想定しています)
2016-05-01 03:15:06 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
このとき対象x∈DからTへのwedgeとは、Dの射の族 σ = { σ_c: x→T(c, c) }_{c∈C} であって、画像の可換性を満たすものを言います。 pic.twitter.com/BBecNsibwR
2016-05-01 03:17:50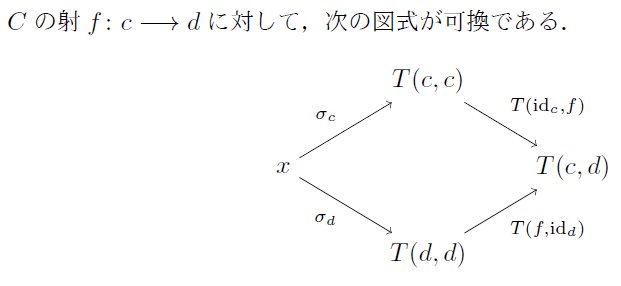 拡大
拡大
 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
例えば F, G: C→D を関手としたとき,Hom(F-, G-): C^op×C→Set という関手を考えます。これはc, c'∈C に対して集合 Hom(Fc, Gc') を与える関手です。
2016-05-01 03:19:54 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
1 = {*} を一点集合として、σを 1 から Hom(F-, G-) へのwedgeとします。σは族 { σ_c: 1→Hom(Fc, Gc) }_{c∈C} であって、さっきの可換性を満たすものです。
2016-05-01 03:21:18 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
T = Hom(F-, G-) の場合、f: c→c' に対して、さっきの図式に出てくる T(id_c, f) とは Hom(F(id_c), G(f)) ですが、これは 後ろから G(f) を合成する写像 G(f)○-: Hom(Fc, Gc)→Hom(Fc, Gc') です
2016-05-01 03:23:40 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
同様にT(f, id) とは 前から F(f) を合成する写像 -○F(f): Hom(Fc', Gc')→Hom(Fc, Gc') です。
2016-05-01 03:24:39 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
これはSetでの図式で、1={*}だから、これが可換というのは、 θ_c := σ_c(*) (写像σ_cの*の行き先) と書くと、 Gf○θ_c = θ_{c'}○Fg ということです。
2016-05-01 03:30:09 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
Gf○θ_c = θ_{c'}○Fg は図式にするとこのようになります pic.twitter.com/BCrIDTCQ9d
2016-05-01 03:31:51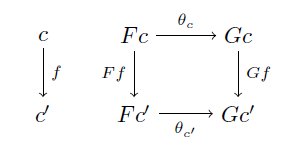 拡大
拡大
 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
これはθが自然変換F⇒Gであることを言っており、つまり、1 から Hom(F-, G-) へのwedgeとは自然変換F⇒Gと同等のものです。
2016-05-01 03:32:42 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
つまり、T: C^op×C→D のエンドとは、組(e, λ)であって、以下を満たすものをいいます: (1) e∈Dは対象である。 (2) λは e から T へのwedgeである。 (3) σが x から T へのwedgeであるならば、p: x→e が一意に存在して(続)
2016-05-01 03:35:36 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
自然変換がwedgeだといいましたが、関手 Hom(F-, G-) のエンドが、 FからGへの自然変換全体がなす集合 Hom_{D^C}(F, G) となることが分かります。(読者の演習問題です)
2016-05-01 03:38:10 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
つまり記号でかくと ∫_cHom(Fc, Gc) = Hom_{D^C}(F, G) であり、射 Fc→Gc を集める(積分する)と自然変換 F⇒G になるといっているんだと思います(たぶん)
2016-05-01 03:39:08 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
C, D, Xを圏として関手 T: C^op×C×X→D を考えます。x∈Xを固定することで、関手 T(-, -, x): C^op×C→D が得られるので、これのエンド ∫_cT(c, c, x)∈D を考えることができます。
2016-05-01 03:41:19 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
すると対応 x |→ ∫_cT(c, c, x)∈D が得られますが、これは関手 ∫_cT(c, c, -): X→D を与えることが分かります。
2016-05-01 03:42:23 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
関手にするのは簡単です。まず k: x→y をXの射としたときに、図式の点線の部分の射を定義する必要がありますが、実践部が全部可換なので、図式を可換にするように、点線の部分の射が一意に取れます(エンドの普遍性) pic.twitter.com/MiiJxT3PSI
2016-05-01 03:44:37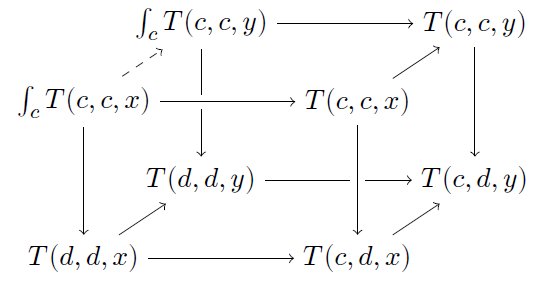 拡大
拡大
 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
さて、今度は4変数の関手 T: C^op×C×X^op×X→D を考えます。もし、必要なエンドが存在すれば、関手 ∫_cT(c, c, -, -): X^op×X→D が得られるので、これのエンド ∫_x∫_cT(c, c, x, x) ∈D を考えることができます。
2016-05-01 03:46:51 V-alg-d(ZZ)
@alg_d
V-alg-d(ZZ)
@alg_d
一方 T を 関手T: (C×X)^op×(C×X)→D だと思えば、エンド ∫_{c,x}T(c, x, c, x)を考えることができます。
2016-05-01 03:47:55